INTRODUCCIÓN
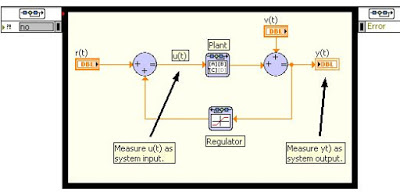
Tiene por objeto obtener el modelo matemático lineal o no lineal de un sistema dinámico a partir de datos experimentales dicho modelo debe reproducir con suficiente exactitud las características dinámicas del proceso objeto de estudio.
La identificación de sistemas es un paso previo al diseño del controlador los cuales pueden ser contínuos o discretos ya sea mediante técnicas clásicas o por variables de estado.
El modelo le permite al diseñador realizar y validar mediante simulación, el ajuste de los parámetros del controlador.
La identificación de sistemas es útil cuando se tienen plantas difíciles de modelar a partir de leyes físicas, como por ejemplo: el estado del tiempo en un espacio controlado.
Cuando se tienen sistemas no lineales o con parámetros variables en el tiempo( identificación de sistemas on-line)
Cuando se requiere de forma rápida y exacta un modelo matemático. Ejemplo: TOOLBOX de identificación de sistemas de MATLAB
Cuando nos enfrentamos a dinámicas no modeladas, plantas nuevas por ejemplo: esto es aquellas a alas que no se les conoce sus características físicas y químicas.
SISTEMA: es toda realidad en la que interactúan variables de diferentes tipos para producir señales observables.
Las señales observables se denominan: salida del sistema y las señales que pueden ser manipuladas libremente se llaman: entradas del sistema y aquellas que ingresan al sistema de forma aleatoria y que no se pueden controlar se llaman perturbaciones.
TIPOS DE MODELOS
MODELO CAJA NEGRA: no se conoce la dinámica del sistema. Pero a futuro se determina la misma a partir de datos experimentales
MODELO CAJA BLANCA: se conoce la dinámica del sistema y se determina a partir de las leyes físico-quimicas.
MODELO CAJA GRIS: es una combinación de los dos anteriores modelos. Por lo general se obtiene un modelo promedio.
MODELOS MENTALES: es conocido como mentales, intuitivos o verbales. Son aquellos que se describen por la experiencia y carecen de formalismo matemático.
MODELOS NO PARAMETRICOS: son aquellos que se caracterizan porque se obtienen a partir de un grafico o una tabla.
Ejemplo: curva de reacción, diagramas de bode, análisis de Fourier.
MODELOS PARAMETRICOS: describen comportamiento del sistema a partir de ecuaciones diferenciales en tiempo continuo.
NOTA:El modelo caja blanca se recomienda usarlo en procesos sencillos de modelar y que no requieran gran exactitud. El modelo caja negra es recomendable usarlo en procesos donde sus parámetros sean difíciles e encontrar y requieran gran exactitud.
RECOMENDACIÓN GENERAL: En la practica, recurrir a la mezcla de las dos formas anteriores para obtener el modelo matemático.
VIDEO 1 INTRODUCCCION
VÍDEO 2 IDENTIFICACIÓN Y CONTROL ADAPTATIVO
VÍDEO 3 MÉTODO DE MÍNIMOS CUADRADOS
VÍDEO 4 SISTEMA NEUMÁTICO POR MEDIO DE LABVIEW
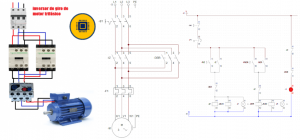
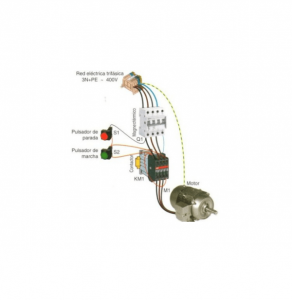
CONTROL AUTOMÁTICO POR LABVIEW DE UN MOTOR TRIFÁSICO
SISTEMA DE ADQUISICIÓN DE DATOS USANDO MATLAB
visita nuestros contenidos relacionados con máquinas eléctricas.
visita nuestros contenidos relacionados con PLC
visita nuestros contenidos relacionados con mediciones e instrumentación.
CONTENIDOS MÁS RELEVANTES.