MODELOS MATEMÁTICOS Y FUNCIONES DE TRANSFERENCIA
MODELOS MATEMÁTICOS Y FUNCIONES DE TRANSFERENCIA
En la reciente práctica de laboratorio se modeló la función de transferencia para un tanque abierto, se diseñó su plano de instrumentación y se resolvieron una serie de funciones de transferencia además de su gráfico en lazo abierto y lazo cerrado ante una entrada en escalón, se experimentó con simulink como herramienta adicional de matlab
OBJETIVOS
GENERAL.
· Obtener la función de transferencia de un sistema a partir del modelado matemático de las leyes físicas que rigen su comportamiento.
ESPECIFICOS
· Describir como se conforman los modelos físicos tomando como ejemplo un sistema masa-resorte-amortiguador
· Analizar el comportamiento de cada una de las respuestas obtenidas de las funciones de transferencia mediante matlab
· Analizar de manera detallada el modelo matemático y el proceso de nivel de líquido presente en uno de los módulos de nivel de laboratorio.
MODELOS MATEMÁTICOS Y FUNCIONES DE TRANSFERENCIA
El primer paso en el proceso de análisis de un sistema físico consiste en deducir un modelo matemático a partir del cual pueden estudiarse las características del sistema. En un sentido muy amplio se puede considerar el modelo como un medio para representar las relaciones entre los componentes del sistema y la teoría para un mismo sistema físico existen varios modelos apropiados.
Una vez que el sistema físico ha sido sustituido por su equivalente modelo lineal, se procede a deducir las ecuaciones del sistema, aplicando las leyes físicas adecuadas. Estas leyes físicas relacionan las variables y parámetros de los componentes, describiendo a través de ecuaciones matemáticas la dinámica de los mismos. Por ejemplo, para los sistemas eléctricos se aplican la ley de ohm, las leyes de Kirchhoff, la ley de Lenz, etc, y para sistemas mecánicos las leyes de movimiento de newton.
Las ecuaciones que representan un sistema físico pueden adoptar diferentes formas. La forma convencional para representar un sistema físico es el empleo de ecuaciones integro-diferenciales las cuales son ecuaciones que poseen operaciones de derivadas e integrales de las variables dependientes en función de la variable independiente t una vez obtenidas las ecuaciones del sistema, se busca obtener la solución de las mismas, las cuales pueden ser resueltas por el método clásico el método operacional o el computacional.
Para un sistema lineal de parámetros constantes, la función de transferencia se define como el cociente de la transformada de Laplace de la salida respecto a la entrada suponiendo las condiciones iniciales iguales a cero
PROCEDIMIENTO EXPERIMENTAL Y RESULTADOS
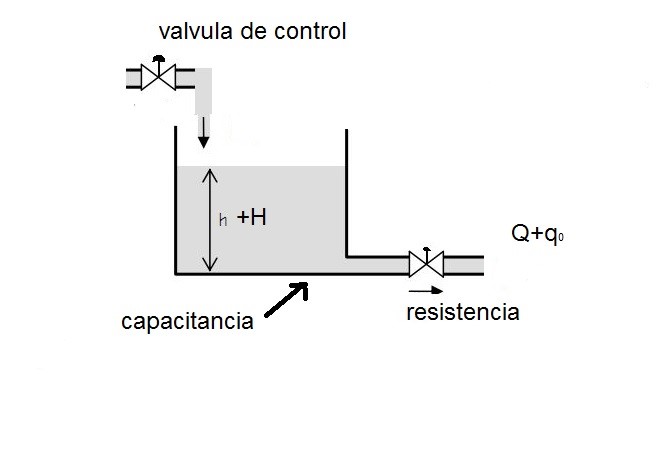
Determinar el modelo matemático y función de transferencia del proceso de nivel de líquido presente en los módulos de laboratorio. Se debe tomar las medidas indicadas por el docente para realizar los cálculos respectivos
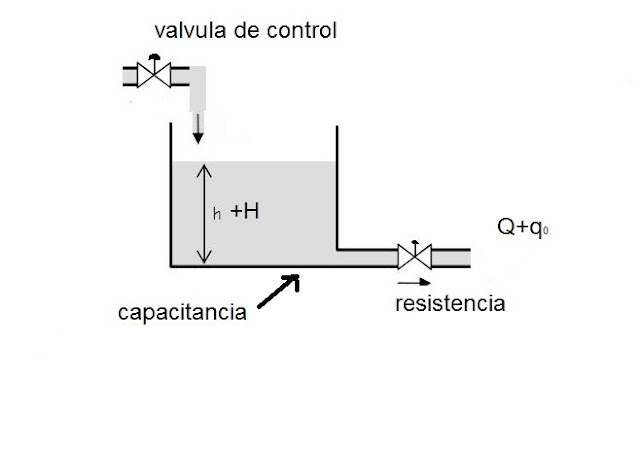
Los parámetros del tanque son los siguientes
Q= velocidad del flujo en estado estable (antes de que haya ocurrido cualquier cambio) m3/s
qi= desviación pequeña de la velocidad de entrada de su valor en estado estable m3/s
qo= desviación pequeña de la velocidad de salida de su valor en estado estable m3/s
H= altura en estado estable (antes que haya ocurrido un cambio), m
h= desviación pequeña de la altura a partir de su valor en estado estable
Un sistema se considera lineal si el flujo es laminar, la ecuación diferencial de este sistema se obtiene del modo siguiente. Dado que el flujo de entrada menos el flujo de salida durante el pequeño intervalo de tiempo dt es igual a la cantidad adicional almacenada en el tanque, observamos que:
A partir de la definición de resistencia, la relación qi y h se obtiene mediante
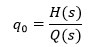
Luego de ello elabore el diagrama de proceso indicando sus componentes y funcionamiento general. Explique el procedimiento realizado y adjunte todos los cálculos y mediciones tomadas.
PROCEDIMIENTO EN SOFTWARE
Digitar el siguiente código en matlab para graficar la respuesta de un sistema ante un estímulo. Use el comando help para entender el funcionamiento de las instrucciones nuevas y del código en general
num=2.4; // numerador de la ft
den=[5 2]; // denominador de la ft
gs=tf(num,den); //crea la ft de lazo abierto
gp=feedback(gs,1); // crea la ft de lazo cerrado
t=0:0.5:20; //determinar tiempo de simulacion
u1=step(gs,t); //genera la respuesta del sistema ante un escalón unitario
u2=step(gp,t); //genera la respuesta del sistema ante un escalón unitario
plot(t,u1,’r’,t,u2,’b’); //generar grafica de respuesta
grid on
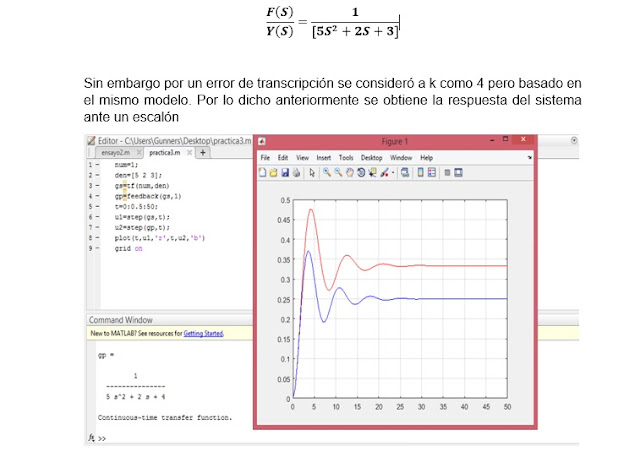
Utilizando las siguientes funciones de transferencia graficar en matlab la respuesta de los sistemas en lazo abierto, lazo cerrado ante una entrada en escalón
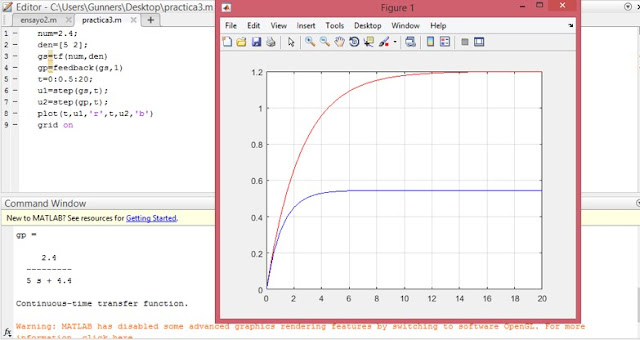
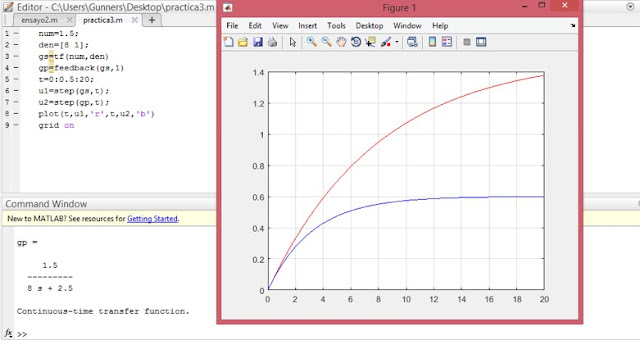
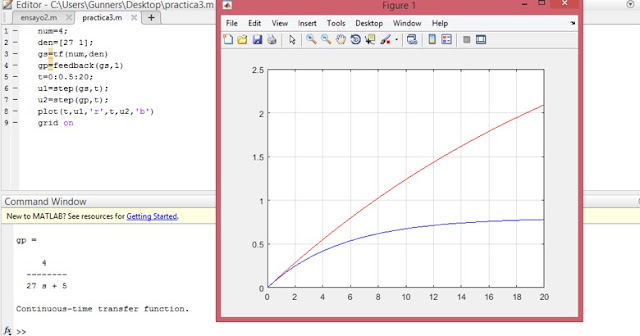
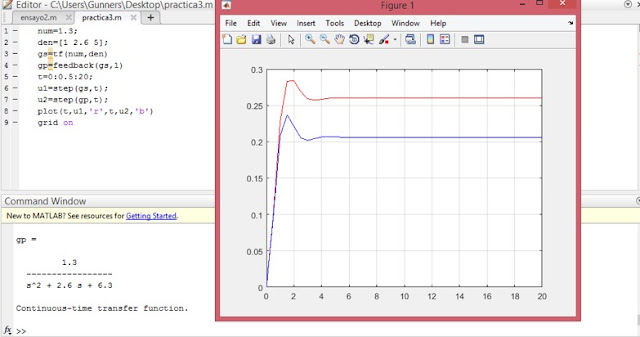
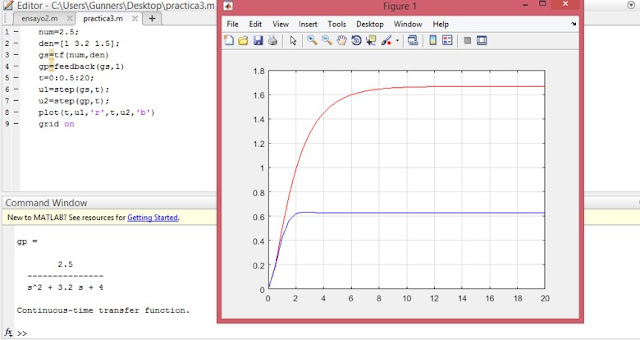
1- Hallar el modelo matemático y función de transferencia del montaje ilustrado a continuación. Primero se plantea la ecuación diferencial y luego asumiendo que tanto la posición y velocidad iniciales son cero, se halla el valor de la posición en función del tiempo
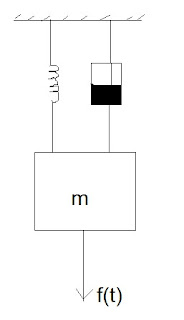
MODELOS MATEMÁTICOS Y FUNCIONES DE TRANSFERENCIA
visita nuestros contenidos relacionados con máquinas eléctricas.
visita nuestros contenidos relacionados con PLC
visita nuestros contenidos relacionados con mediciones e instrumentación.
CONTENIDOS MÁS RELEVANTES.
Muchas gracias por tu aportación. Feliz semana.
Super el repaso de estos temas son de mucha ayuda…. Gracias !!!
I think this is one of the most important information for me.
And i’m glad reading your article. But want to remark on few general things,
The website style is perfect, the articles is really great : D.
Good job, cheers