CIRCUITOS ELÉCTRICOS: LEYES DE KIRCHHOFF
las leyes de Kirchhoff.
En este artículo hablaremos de la forma más detallada posible acerca de las leyes de un físico prusiano muy famoso nacido en la antigua Rusia llamado Gustav Robert Kirchhoff. Sin duda la aplicación de estas leyes a lo largo de la historia ha sido precursora en el análisis y desarrollo de circuitos y sistemas eléctricos- electrónicos hasta los tiempos modernos.
Antes que nada, Gustav fue un físico interesado principalmente por los estudios de termodinámica, espectroscopia y ¡por supuesto! ELECTRICIDADun campo de mucha innovación y desarrollo que hasta los tiempos de hoy sigue teniendo auge a nivel industrial, económico y científico. La electricidad es necesaria para todo: para alimentar motores, bombillas incandescentes, conectar televisores, incluso para energizar la fuente de voltaje que posee este computador y redactarles este post que con mucho cariño les entrega esta valiosa información y conocimiento para ustedes aficionados, amantes a la electrónica y a la tecnología.
Las leyes de Kirchhoff son vitales para el análisis de circuitos eléctricos tanto en corriente directa como en corriente alterna. Básicamente se componen de dos leyes: LEY DE VOLTAJE Y LEY DE CORRIENTE DE KIRCHHOFF, en vez de voltaje se puede expresar la palabra: LEY DE TENSIÓN O LEY DE DIFERENCIA DE POTENCIAL O LEY DE POTENCIALpuesto que tensión es lo mismo. De igual manera se puede abreviar como(LVK) (LCK) donde LVK es ley de voltaje y LCKes ley de corriente y de Kirchhoff ¡POR SUPUESTO!
La ley de voltaje de Kirchhoff establece que la SUMATORIA de las corrientes o mejor LA SUMA DE LAS CORRIENTES que entran alrededor de una rama o un lazo que está completamente cerrado es igual a cero ¡ muy bien! En ese caso debemos analizar como se dá esto porque pudo haber ocurrido que mucha gente o muchos de los que leen este post no lo entendieron y créanme ¡ SI ME TOCA ENSEÑAR MATEMÁTICAS PARA QUE ENTIENDAN ESTO TAN SENCILLO LO HAGO! Porque la idea es que la teoría encaje correctamente con la práctica lo más claro posible.
EXPLICACIÓN.
Consideremos por un momento que la corriente eléctrica se va a llamar (I) donde I significa ¡corriente! Aunque también signifique intensidad ¿vale?. ¡BUENO EMPECEMOS!
Imagina por un momento que todas las corrientes se suman por un momento. Por decir algo, corriente 1 más corriente 2, más corriente 3, más corriente 4, más corriente 5 es igual a cero. ¡ ahora! No necesariamente son cinco corrientes, pueden ser miles o millones pero ¡ TU SABES QUE EN LA VIDA REAL NO HAY MILLONES DE CABLES ENTRANDO A UN SOLO PUNTO Y DECIR I1 HASTA I infinito!Ahora bien. Expresa matemáticamente teniendo en cuenta que las corrientes se llaman I, ¿COMO LO HARÍAS? ¡ PUES YO LO HARÍA ASÍ!
I1 + I2 + I3 +I4 +I5=0
¿Si ves que es muy fácil? Expresamos en palabras los valores de las corrientes y los colocamos con letras, pero mira que las denotamos con números como por ejemplo I1 I2 I3 I4 I5. Woow es muy sencillo. Ahora vamos a expresarlo en términos de sumatoria para que se aprecie matemáticamente y ustedes puedan observar como hace magia la matemática. Bueno antes que nada el operador sumatoria es un símbolo o yo llamo jerarquía matemática que lo que simplemente hace es representar la suma de una cantidad de números, datos, valores, elementos y entregar un resultado al final. Tiene alta aplicabilidad en asignaturas como por ejemplo CÁLCULO INTEGRAL, SISTEMAS Y SEÑALES, MATEMÁTICAS ESPECIALES, ECONOMÍA Y FINANZAS y un sinnúmero de campos que conocerás con mucha dedicación investigación, desarrollo y disciplina. Debes alejar un poco la pereza si deseas lograr todo esto.
La expresión matemática que modela lo representado anteriormente está denotado de la siguiente forma:
Como te puedes dar cuenta en la imagen que visualizas lo anterior representa la ecuación 1 modelada con la letra I y sumada. Cabe mencionar que N es el número de ramas conectadas al nodo en este caso podrían considerarse como resistencias, condensadores, cualquier elemento y n es la n-ésima corriente de nodo. Ya dicho esto vamos a enunciar esta ecuación de la siguiente forma tal como lo hizo este gran científico.
LA SUMA ALGEBRAICA DE LAS CORRIENTES QUE ENTRAN A UN NODO ES IGUAL A CERO.
Si te das cuenta, la palabra clave es nodo. Y esta palabra la utilizaremos con mayor frecuencia cuando expliquemos análisis de nodos más específicamente de CORRIENTES DE NODO. No solo en el área de circuitos eléctricos sino también en el campo de los amplificadores operacionales. LA RUTA ES BASTANTE LARGA.
Ahora bien. Cabe mencionar que hay corrientes que entran a un nodo. Pero también puede ocurrir que haya corrientes que salen del nodo. Esas corrientes que entran pueden ser consideradas positivas y las que salen pueden considerarse negativas. Si por ejemplo en un nodo entran unas corrientes, deben haber unas que salgan. Está representada mediante la siguiente ecuación.
Muy bien. Como toda teoría debe ir soportada por algo que se entienda pasamos de forma inmediata a la práctica matemática para luego ir a la práctica experimental.
Ejemplo.
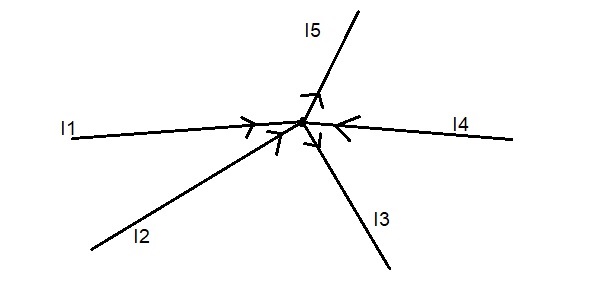
Expresar la ecuación que modela la siguiente representación de corrientes.
Solución.
Lo primero es establecer o identificar cual es el nodo. Si observas claramente, el nodo es el punto que ves en el centro y es donde conectan todas las corrientes. Ahora bien identifica cuales son las corrientes que entran al punto y cuales son las que salen:
Las corrientes que entran al nodo son I1 I2 I4 y las corrientes que están saliendo del nodo son: I3 e I5 se observa claramente por el sentido que tienen las flechas. Ahora bien. Basado en la ecuación anterior:
Simplemente lo que hacemos es ubicar las corrientes que entran del lado donde se encuentra sumatoria de corrientes que entran y del lado donde salen las corrientes colocamos las corrientes que están saliendo del nodo. El reemplazo de las sumatorias nos modela la siguiente ecuación.
I1 +I2 +I4= I3 + I5
Te preguntarás: ¿ y ahora que sigue? Pues no sigue absolutamente nada puesto que ya la ecuación queda modelada. Pero bien! Si deseas puedes expresar esta ecuación reemplazando los valores que se encuentran a la derecha con signo contrario en la parte izquierda. Si haces eso la ecuación te quedará de la siguiente forma:
I1 +I2 +I4= I3 + I5
I1 +I2 +I4– I3 – I5= 0
si bien vemos como queda la nueva expresión aquí no se hace más nada puesto que esto nos servirá más adelante para el análisis de mallas y nodos y apenas nos estamos adentrando al maravilloso mundo de los circuitos
felicidades. Hemos dado un pequeño paso para analizar las corrientes de un circuito eléctrico y poco a poco nos adentramos al maravilloso mundo de los circuitos eléctricos. Ahora vamos con los voltajes de un circuito eléctrico. Kirchhoff ya había enunciado la ley y vamos a hacerlo al mejor estilo que lo puede hacer este gran científico.
La suma algebráica de los voltajes, tensiones, potenciales, alrededor de una trayectoria cerrada o lazo cerrado es igual a cero.
¡NO ENTENDÍ NADA! ¿ QUE HAGO?
Tranquilo no es nada difícil, de hecho es algo muy sencillo. Imagina por un momento que la variable física voltaje está representado por la letra (V) y que estás sumando unas baterías o pilas alrededor de un circuito. Ahora imagina que tienes que sumar todos los voltajes de dichas pilas para tener un voltaje total suma por ejemplo: 5 valores de voltaje identificados como V1, V2,V3,V4,V5.
Ahora une con el signo más igualando a cero los valores de voltaje mencionados anteriormente y de la siguiente forma:
V1+ V2+V3 +V4 +V5 =0
Ahora que has hecho esto, es hora de modelar la ecuación que represente en forma matemática con el operador sumatoria esta ecuación.
Básicamente lo que nos está diciendo esta ecuación es que la sumatoria de los voltajes es igual a cero. Lo mismo que enunciaba la segunda ley de kirchoff que lo describimos en letra cursiva. Pero solo lo hice para que te dieras cuenta que realmente llegamos a lo mismo.
Bueno: ahora de la teoría básica pasemos a un ejercicio:
Tenemos tres valores de baterías o fuentes de voltaje conectadas en serie. Si te das cuenta los valores de cada una de las baterías son: 26 volts, 34 volts y 9 volts. Si usted conecta en serie estas baterías va a tener a la salida un valor equivalente a 69 volts demostrado en la siguiente solución matemática
V1+ V2+V3 =0
26V +34 V + 9V = 69 volts
Ahora mediante un corto video de simulación vamos a comprobar lo dicho en teoría Para este ejercicio emplearemos proteus como herramienta de simulación.
Mira el vídeo para que observes como ocurre esto.
feliz día
CONTENIDOS MÁS RELEVANTES.