Respuesta temporal de varios sistemas de control empleando MATLAB.

Para mostrar la respuesta temporal de varios sistemas de control utilizando MATLAB, se tienen en cuenta varias consideraciones.

1. Se crea un menú con la función propia de MATLAB que se llama menu(‘opcion1′,’Opcion2’)

2. Por cada opción del menu, se presenta la función de transferencia del sistema y su respectiva gráfica con sus características

3. Finalmente se realiza la simulación

Análisis

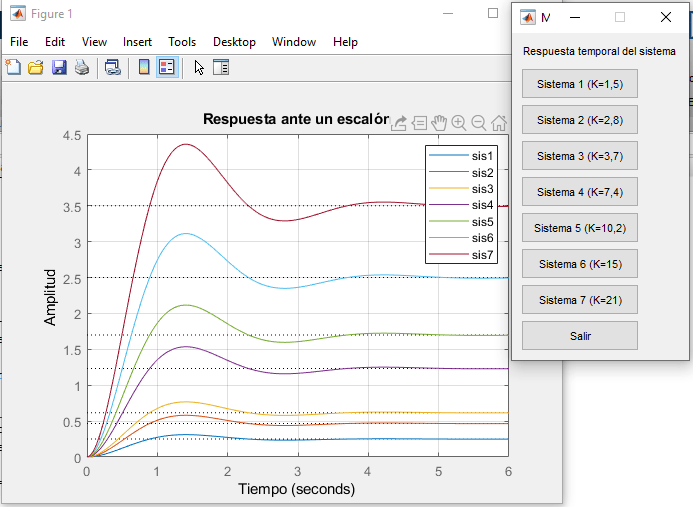
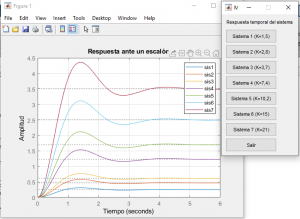
Los sistemas son de segundo orden y sin retardo. Se puede percibir en las gráficas, que el valor de K varía; lo que genera que se presenten máximos sobre impulsos y el tiempo pico aumente.

Además, los sistemas no se estabilizan en el escalón unitario, por ende no son estables y no hay tiempo de establecimiento.

CODIGO FUENTE.

%Respuesta ante una entrada escalón 
%Nat Arenas L 
% Y(S)/R(S)= K/S^2+2S+6
 

K=menu('Respuesta temporal del sistema', 'Sistema 1 (K=1,5)', 'Sistema 2 (K=2,8)','Sistema 3 (K=3,7)','Sistema 4 (K=7,4)','Sistema 5 (K=10,2)','Sistema 6 (K=15)','Sistema 6 (K=21)','Salir')
while(K)
    if K==1
        n=[1.5];  %Valor del numerador de la FT
        d=[1 2 6]; %Valor del denominador de la FT
        sis1=tf(n,d) %Permite crear la función de trasnferencia 
        step(sis1)  %Genera el estimulo del sistema 
        legend()    %Genera una etiqueta de texto para indentificar la gráfica
        title('Respuesta ante un escalón') %Función para el título de la gráfica 
        xlabel('Tiempo') %Función para el título del eje x
        ylabel('Amplitud') %Función para el título del eje y
        grid on %Poner la cuadrícula 
        hold on %Conserva la gráfica actual
    end
 
   if K==2
       n=[2.8];   %Valor del numerador de la FT
       d=[1 2 6]; %Valor del denominador de la FT
       sis2=tf(n,d)  %Permite crear la función de trasnferencia 
       step(sis2)    %Genera el estimulo del sistema 
       legend()      %Genera una etiqueta de texto para indentificar la gráfica
       title('Respuesta ante un escalón')  %Función para el título de la gráfica
       xlabel('Tiempo') %Función para el título del eje x
       ylabel('Amplitud')  %Función para el título del eje y
       grid on %Poner la cuadrícula 
       hold on %Conserva la gráfica actual
   end 

   if K==3
       n=[3.7];  %Valor del numerador de la FT
       d=[1 2 6]; %Valor del denominador de la FT
       sis3=tf(n,d) %Permite crear la función de trasnferencia 
       step(sis3)   %Genera el estimulo del sistema 
       legend()     %Genera una etiqueta de texto para indentificar la gráfica
       title('Respuesta ante un escalón') %Función para el título de la gráfica
       xlabel('Tiempo') %Función para el título del eje x
       ylabel('Amplitud') %Función para el título del eje y
       grid on  %Poner la cuadrícula 
       hold on  %Conserva la gráfica actual
   end
  
   if K==4
       n=[7.4];  %Valor del numerador de la FT
       d=[1 2 6]; %Valor del denominador de la FT
       sis4=tf(n,d) %Permite crear la función de trasnferencia 
       step(sis4)   %Genera el estimulo del sistema 
       legend()     %Genera una etiqueta de texto para indentificar la gráfica
       title('Respuesta ante un escalón') %Función para el título de la gráfica
       xlabel('Tiempo') %Función para el título del eje x
       ylabel('Amplitud') %Función para el título del eje y
       grid on  %Poner la cuadrícula 
       hold on  %Conserva la gráfica actual
   end
   
    if K==5
       n=[10.2];  %Valor del numerador de la FT
       d=[1 2 6]; %Valor del denominador de la FT
       sis5=tf(n,d) %Permite crear la función de trasnferencia 
       step(sis5)   %Genera el estimulo del sistema 
       legend()     %Genera una etiqueta de texto para indentificar la gráfica
       title('Respuesta ante un escalón') %Función para el título de la gráfica
       xlabel('Tiempo') %Función para el título del eje x
       ylabel('Amplitud') %Función para el título del eje y
       grid on  %Poner la cuadrícula 
       hold on  %Conserva la gráfica actual
    end
    
    if K==6
       n=[15];  %Valor del numerador de la FT
       d=[1 2 6]; %Valor del denominador de la FT
       sis6=tf(n,d) %Permite crear la función de trasnferencia 
       step(sis6)   %Genera el estimulo del sistema 
       legend()     %Genera una etiqueta de texto para indentificar la gráfica
       title('Respuesta ante un escalón') %Función para el título de la gráfica
       xlabel('Tiempo') %Función para el título del eje x
       ylabel('Amplitud') %Función para el título del eje y
       grid on  %Poner la cuadrícula 
       hold on  %Conserva la gráfica actual
    end
   
     if K==7
       n=[21];  %Valor del numerador de la FT
       d=[1 2 6]; %Valor del denominador de la FT
       sis7=tf(n,d) %Permite crear la función de trasnferencia 
       step(sis7)   %Genera el estimulo del sistema 
       legend()     %Genera una etiqueta de texto para indentificar la gráfica
       title('Respuesta ante un escalón') %Función para el título de la gráfica
       xlabel('Tiempo') %Función para el título del eje x
       ylabel('Amplitud') %Función para el título del eje y
       grid on  %Poner la cuadrícula 
       hold on  %Conserva la gráfica actual
    end
   
    if K==8
        break;  %Para salir del menu
    end 

   K=menu('Respuesta temporal del sistema', 'Sistema 1 (K=1,5)', 'Sistema 2 (K=2,8)','Sistema 3 (K=3,7)','Sistema 4 (K=7,4)','Sistema 5 (K=10,2)','Sistema 6 (K=15)','Sistema 7 (K=21)','Salir')
end
 



GRÁFICA EN MATLAB DE LOS SISTEMAS MOSTRADOS EN PANTALLA.