CONTROL AUTOMÁTICO: ÁLGEBRA DE BLOQUES DE CONTROL
INTRODUCCIÓN
En la reciente práctica de laboratorio se trabajó con matlab específicamente con la herramienta adicional llamada simulink el cual es destacada como un complemento de matlab que reemplaza la programación convencional y se enfoca en la programación visual de algoritmos matemáticos además de ser considerado un lenguaje de alto nivel dentro de los cuales destacamos abstracción de fenómenos físicos, sistemas de control, electrónica, sistemas de procesamiento de señales, ingeniería en control y robótica. Por tanto para el desarrollo de esta práctica se efectuó el montaje de cada uno de los bloques propuestos por la práctica de laboratorio, se procedió a realizar simulaciones de cada uno de los sistemas sometiendo cada uno a una estimulación con entrada escalón y se analizaron las bondades de usar simulink respecto a matlab.
OBJETIVOS.
Simular en software los sistemas de control representados y simplificarlos a partir de los diagramas de bloques.
MARCO TEÓRICO.
Un sistema de control puede tener varios componentes. Para mostrar las funciones que lleva a cabo cada componente de la ingeniería de control, por lo general se usa una representación denominada diagrama de bloques.
Un diagrama de bloques de un sistema es una representación grafica de las funciones que lleva a cabo cada componente y el flujo de señales.
Tal diagrama muestra las relaciones existentes entre los diversos componentes. A diferencia de una representación matemática puramente abstracta, un diagrama de bloques funcionales.
El bloque funcional o simplemente bloque es un símbolo para representar la operación matemática que sobre la señal de entrada hace el bloque para producir la salida. Las funciones de transferencia de los componentes por lo general se introducen en los bloques correspondientes, que se conectan mediante flechas para indicar la dirección del flujo de señales. Observe que la señal solo puede pasar en la dirección de las flechas.
Por lo tanto, un diagrama de bloques de un sistema de control muestra explícitamente una propiedad unilateral.
La figura muestra los elementos principales de un diagrama de bloques. La punta de la flecha que señala el bloque indica la entrada, y la punta de la flecha que se aleja del bloque representa la salida. Tales flechas se conocen como señales.
Un diagrama de bloques puede ser simplificado a partir de operaciones algebraicas especiales.
CONTROL AUTOMÁTICO: LABORATORIO DE ÁLGEBRA DE BLOQUES DE CONTROL
Realizar la representación gráfica de los anteriores diagramas de bloques en simulink, obtenga la respuesta del sistema ante una entrada escalón.
DIAGRAMA NÚMERO 1.
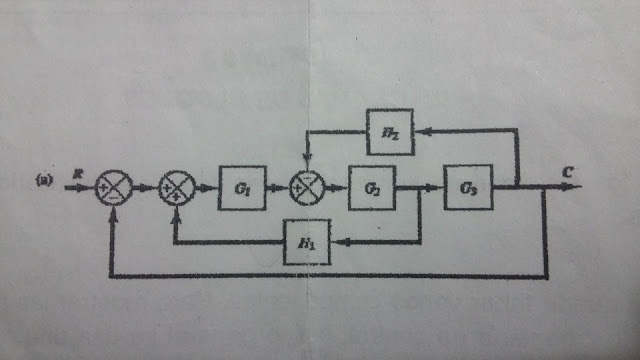
CONTROL AUTOMÁTICO: LABORATORIO DE ÁLGEBRA DE BLOQUES DE CONTROL
REPRESENTACIÓN DEL ANTERIOR SISTEMA DE DIAGRAMA DE BLOQUES EN SIMULINK.

La respuesta del sistema ante una entrada escalón. Se comporta de la siguiente manera.
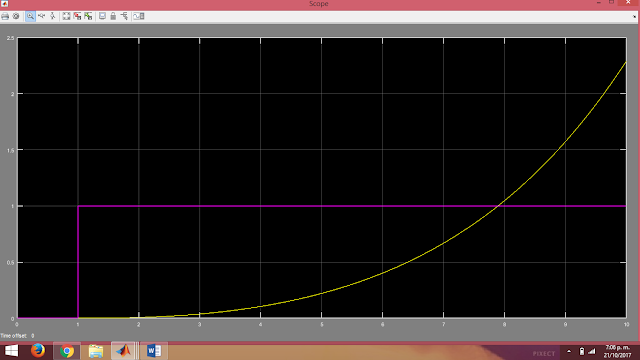
DIAGRAMA NÚMERO 2.
REPRESENTACIÓN DEL ANTERIOR SISTEMA DE DIAGRAMA DE BLOQUES EN SIMULINK.
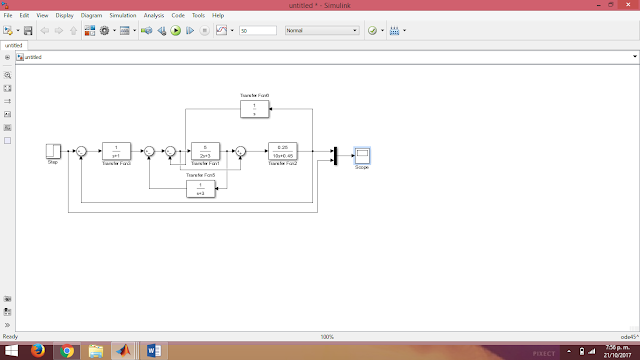
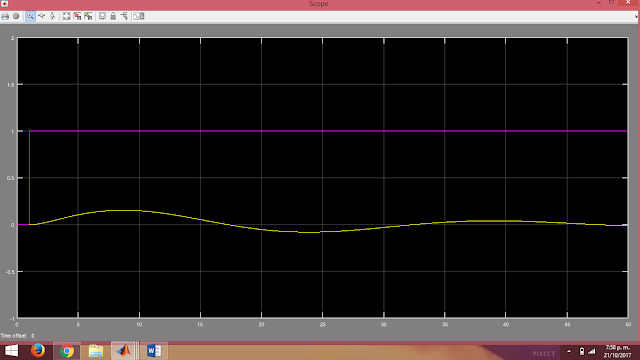
CONTROL AUTOMÁTICO: LABORATORIO DE ÁLGEBRA DE BLOQUES DE CONTROL
Realizar la representación gráfica de la simplificación de los anteriores diagramas de bloques en simulink, obtenga la respuesta del sistema ante una entrada escalón y compare con respecto a la respuesta obtenida en el numeral anterior.
De la simplificación del diagrama de bloques por operaciones matemáticas nos quedó así para el primer sistema
La respuesta de esta simplificación ante una entrada escalón es:
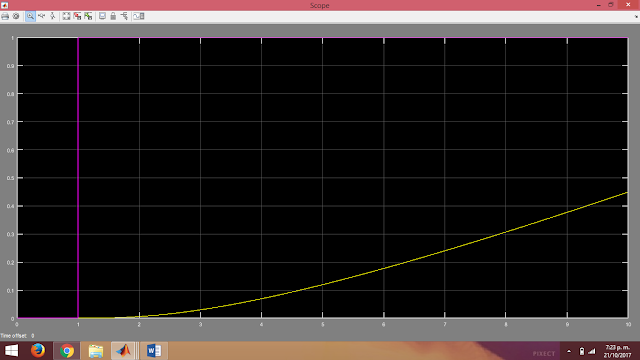
De la simplificación del diagrama de bloques a través de operaciones entre bloques y sus propiedades nos dio de la siguiente forma.
Ya para la representación gráfica de la simplificación del diagrama de bloques se verá en la siguiente imagen.
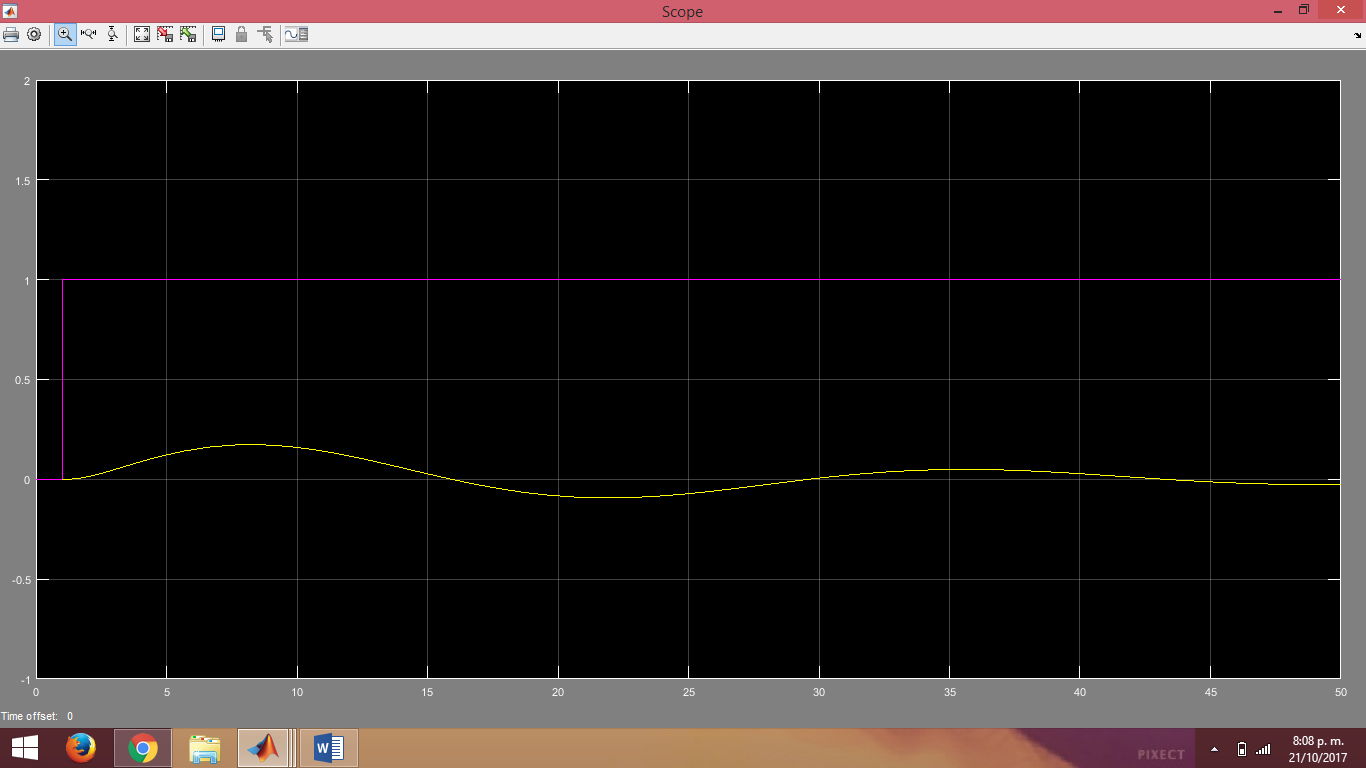
ANÁLISIS MATEMÁTICO
Para el bloque 1
Procedemos a simplificar
SEGUNDO DIAGRAMA DE BLOQUES
CONCLUSIONES.
· Se aprendió a realizar diagramas de bloques en simulink, utilizar ciertos componentes de los muchos que tiene. En este caso para una entrada escalón, también ara ingresar una función de transferencia, como se puede visualizar gráficamente la gráfica de la entrada escalón vs la respuesta del sistema ante esa entrada.
· Se refuerza los conocimientos vistos en la teoría acerca de la simplificación de diagramas de bloques y sus propiedades.
· Para el diagrama de bloques número 1 los resultados no fueron muy buenos ya que la gráfica que nos dio sin simplificar da muy diferente a la gráfica del diagrama de bloques simplificado. Se probó paso a paso y notamos que en el primer paso que se realizó en la simplificación que fue un traslado de punto de suma, el cual está bien aplicada esta propiedad y que anteriormente lo hemos hecho mucho en la teoría. Probamos en simulink con este primer paso y de entrada está variando la gráfica. Basado en los conocimientos vistos en la teoría puedo afirmar que los cálculos están buenos.
· En el diagrama dos sucede todo lo contrario tanto el sistema simplificado da la misma respuesta que el sistema sin simplificar.
BIBLIOGRAFÍA
OGATA, KATSUHIKO. Ingeniería de Control Moderna. 3a edición. Prentice-Hall. Hispanoamericana, S.A.. 1998.
visita nuestros contenidos relacionados con máquinas eléctricas.
visita nuestros contenidos relacionados con PLC
visita nuestros contenidos relacionados con mediciones e instrumentación.
CONTENIDOS MÁS RELEVANTES.