LEY DE CORRIENTE DE KIRCHHOFF
El día de hoy vamos a resolver una serie de ejercicios relacionados con la ley de corriente de Kirchhoff los cuales iremos explicando de manera detallada y analizando de donde salen las variables correspondientes para evitar cometer errores y hacer las cosas bien al momento de enfrentarnos a un taller o a una práctica de laboratorio, sin más preámbulo aquí le presentamos los ejercicios.
EJERCICIO 1
Se pide aplicar la ley de corriente de Kirchhoff en este circuito específicamente hallando la corriente Io y el voltaje Vo en el circuito que aparece en la siguiente figura:
antes de empezar a resolver este circuito es importante aclarar respecto a las fuentes dependientes, que estas existen físicamente pero en componentes electrónicos como transistores y otros dispositivos semiconductores.
Empezamos con el análisis de este circuito aplicando ley de corriente de Kirchhoff al nodo denotado con la letra a
De esta forma:
Despejando Io nos queda de la siguiente forma
Haciendo dividir a Io nos queda:
Luego calculando el voltaje en la resistencia de 4 ohms nos queda de la siguiente forma:
de esta manera hemos calculado las variables pedidas por el ejercicio
EJERCICIO 2
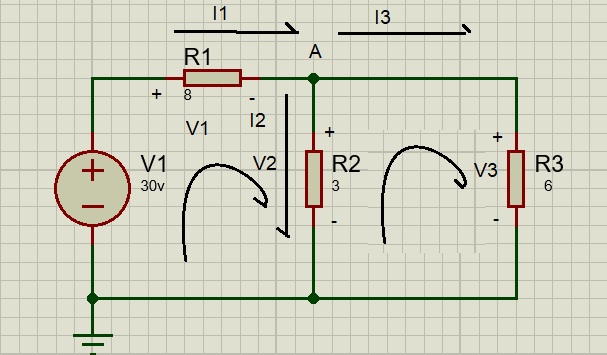
calcular las corrientes y los voltajes en el circuito presentado en la figura:
se aplica las leyes de ohm y Kirchhoff. Por efecto de la ley de ohm obtenemos las siguientes ecuaciones:
Puesto que el voltaje y la corriente de cada resistencia están relacionados por la ley de ohm como se indica, en realidad se están buscando 3 cosas (V1-V2-V3) (I1-I2-I3) en el nodo A da como resultado el siguiente análisis de corrientes. (ojo) recordar que las corrientes que entran es igual a las que salen
Si se aplica ley de voltaje de Kirchhoff al lazo 1 nos queda de la siguiente forma:
Se expresa esto en términos de I1 e I2 como en la ecuación de los voltajes para obtener lo siguiente:
Y hacemos lo siguiente:
Al aplicar ley de voltaje de Kirchhoff al lazo 2 nos queda lo siguiente:
Y como era de esperarse, ya que estas dos resistencias están en paralelo. Se expresa V1 y V2 en términos de I1 e I2 y nos queda de la siguiente forma:
Sustituimos en la ecuación planteada como ley de corriente de Kirchhoff y nos queda de la siguiente forma:
O también I2=2A
Y reemplazamos y obtenemos las respuestas.
DESCARGA EL ARCHIVO PDF AQUÍ
CONTENIDOS MÁS RELEVANTES.