Pasos para tener en cuenta:
1. Se crea un menú con el switch case
2. Por cada opción del menú, se realiza la función de transferencia del sistema y la gráfica con sus características
3. Finalmente se realiza la simulación
Análisis
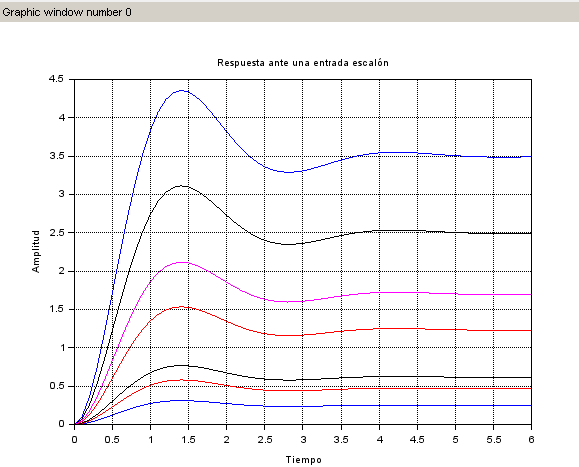
En las gráficas se puede concluir:
1. El sistema es de segundo orden, porque presentan dos polos.
2. Son sin retardo, porque no presentan algún tiempo muerto.
3. La K varía, generando máximos sobre impulsos y un tiempo de pico cada vez mayor.
4. No hay estabilidad en los sistemas. Hay sistemas que están por encima y por debajo del escalón unitario
programa elaborado en SCILAB
//Respuesta temporal para el siguiente sistema K/(S^2+2S+6))
//Nat Arenas L
for i=1:8
disp(' Respuesta temporal del sistema ')
disp('1.Sistema 1 K=1,5')
disp('2.Sistema 2 K=2,8')
disp('3.Sistema 3 K=3,7')
disp('4.Sistema 4 K=7,4')
disp('5.Sistema 5 K=10,2')
disp('6.Sistema 6 K=15')
disp('7.Sistema 7 K=21')
disp('SALIR')
K=input("Ingrese un numero del 1 hasta el 8: ")
switch(K)
case 1
K==1
s=poly(0,"s"); //Construye el polinomio con la variable s.
num=1.5;
den=s^2+2*s+6;
sis1 = syslin('c',num,den); //La c indica el sistema en tiempo continuo.
//Para generar la función de transferencia
t=0:0.1:6 //Indica el tiempo(eje x)
plot(t,csim('step',t,sis1)) //Función para generar el estimulo al sistema
legend(sis1)
title("Respuesta ante una entrada escalón") //Función para generar el título de la gráfica
xlabel("Tiempo") //Función que indica el título del eje x
ylabel("Amplitud") //Función que indica el título del eje y
xgrid() //Para la cuadrícula
set(gca(),"auto_clear","off") //Para conservar la gráfica actual
case 2
K==2
s=poly(0,"s"); //Construye el polinomio con la variable s.
num=2.8;
den=s^2+2*s+6;
sis2 = syslin('c',num,den); //La c indica el sistema en tiempo continuo.
//Para generar la función de transferencia
t=0:0.1:6 //Indica el tiempo(eje x)
plot(t,csim('step',t,sis2),'r') //Función para generar el estimulo al sistema
title("Respuesta ante una entrada escalón") //Función para generar el título de la gráfica
xlabel("Tiempo") //Función que indica el título del eje x
ylabel("Amplitud") //Función que indica el título del eje y
xgrid() //Para la cuadrícula
set(gca(),"auto_clear","off") //Para conservar la gráfica actual
case 3
K==3
s=poly(0,"s"); //Construye el polinomio con la variable s.
num=3.7;
den=s^2+2*s+6;
sis3 = syslin('c',num,den); //La c indica el sistema en tiempo continuo.
//Para generar la función de transferencia
t=0:0.1:6 //Indica el tiempo(eje x)
plot(t,csim('step',t,sis3),'k') //Función para generar el estimulo al sistema
title("Respuesta ante una entrada escalón") //Función para generar el título de la gráfica
xlabel("Tiempo") //Función que indica el título del eje x
ylabel("Amplitud") //Función que indica el título del eje y
xgrid() //Para la cuadrícula
set(gca(),"auto_clear","off") //Para conservar la gráfica actual
case 4
K==4
s=poly(0,"s"); //Construye el polinomio con la variable s.
num=7.4;
den=s^2+2*s+6;
sis4 = syslin('c',num,den); //La c indica el sistema en tiempo continuo.
//Para generar la función de transferencia
t=0:0.1:6 //Indica el tiempo(eje x)
plot(t,csim('step',t,sis4),'r') //Función para generar el estimulo al sistema
title("Respuesta ante una entrada escalón") //Función para generar el título de la gráfica
xlabel("Tiempo") //Función que indica el título del eje x
ylabel("Amplitud") //Función que indica el título del eje y
xgrid() //Para la cuadrícula
set(gca(),"auto_clear","off") //Para conservar la gráfica actual
case 5
K==5
s=poly(0,"s"); //Construye el polinomio con la variable s.
num=10.2;
den=s^2+2*s+6;
sis5 = syslin('c',num,den); //La c indica el sistema en tiempo continuo.
//Para generar la función de transferencia
t=0:0.1:6 //Indica el tiempo(eje x)
plot(t,csim('step',t,sis5),'m') //Función para generar el estimulo al sistema
title("Respuesta ante una entrada escalón") //Función para generar el título de la gráfica
xlabel("Tiempo") //Función que indica el título del eje x
ylabel("Amplitud") //Función que indica el título del eje y
xgrid() //Para la cuadrícula
set(gca(),"auto_clear","off") //Para conservar la gráfica actual
case 6
K==6
s=poly(0,"s"); //Construye el polinomio con la variable s.
num=15;
den=s^2+2*s+6;
sis6 = syslin('c',num,den); //La c indica el sistema en tiempo continuo.
//Para generar la función de transferencia
t=0:0.1:6 //Indica el tiempo(eje x)
plot(t,csim('step',t,sis6),'k') //Función para generar el estimulo al sistema
title("Respuesta ante una entrada escalón") //Función para generar el título de la gráfica
xlabel("Tiempo") //Función que indica el título del eje x
ylabel("Amplitud") //Función que indica el título del eje y
xgrid() //Para la cuadrícula
set(gca(),"auto_clear","off") //Para conservar la gráfica actual
case 7
K==7
s=poly(0,"s"); //Construye el polinomio con la variable s.
num=21;
den=s^2+2*s+6;
sis7 = syslin('c',num,den); //La c indica el sistema en tiempo continuo.
//Para generar la función de transferencia
t=0:0.1:6 //Indica el tiempo(eje x)
plot(t,csim('step',t,sis7),'b') //Función para generar el estimulo al sistema
title("Respuesta ante una entrada escalón") //Función para generar el título de la gráfica
xlabel("Tiempo") //Función que indica el título del eje x
ylabel("Amplitud") //Función que indica el título del eje y
xgrid() //Para la cuadrícula
set(gca(),"auto_clear","off") //Para conservar la gráfica actual
case 8
K==8
break;
legend('sis1','sis2','sis3','sis4','sis5','sis6','sis7') //Etiquetas de texto para
else
disp('Invalido')
end
end
GRAFICA OBTENIDA EN SCILAB
CONTENIDOS RELACIONADOS.
visita nuestros contenidos relacionados con máquinas eléctricas.
visita nuestros contenidos relacionados con PLC
visita nuestros contenidos relacionados con mediciones e instrumentación.
CONTENIDOS MÁS RELEVANTES.