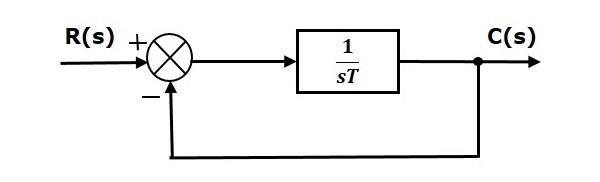
Básicamente depende de dos cosas que son: la entrada del sistema y el orden del sistema
Para respuesta temporal en plantas de primer orden tenemos:
Su transformada de Laplace es:
RESPUESTA TEMPORAL DE SISTEMAS DE CONTROL
Y el modelo del sistema es:
RESPUESTA TEMPORAL DE SISTEMAS DE CONTROL
La anterior ecuación es la expresión general de una salida para un sistema de primer orden ante entrada escalón unitario
Siendo el sistema
Gráficamente.
Si R(s)= 1/s es un escalón unitario.
Aplicando transformada inversa de Laplace,
De Ta 2T el estado se comporta como transitorio y el efecto del polo es bastante considerable
RESPUESTA TEMPORAL DE SISTEMAS DE CONTROL
De 3Ta 5T el estado es estacionario. El efecto del polo desaparece con el tiempo
CARACTERISTICAS DEL SISTEMA
VALOR DE LA SALIDA EN ESTADO ESTABLE (Yee) es el valor que toma la salida y(t) cuando
T tiende a infinito
yee=k
CONSTANTE DE TIEMPO (T): es el tiempo que tarda en alcanzar el 63.2% de la salida en estado estable de yee
TIEMPO DE ESTABLECIMIENTO (ts)tiempo que tarda en alcanzar yee a 4T o 5T
EJEMPLO: para el siguiente sistema ante una entrada escalón unitario y escalón de magnitud seis se debe determinar.
a) Constante de tiempo
b) Tiempo de establecimiento
c) Valor de la salida en estado estable
d) Expresión matemática de la salida
e) Representación gráfica de la salida y de la ubicación de polos
SOLUCIÓN
1 se normaliza la ecuación dividiendo por 6
Dividiendo por 6 que corresponde a la magnitud y escalón 6 nos queda el modelo de la siguiente forma:
Por lo tanto, la constante de tiempo es 0.5seg
Los tiempos de establecimiento son de 4To 5T
El valor de la salida en estado estable yee=1.25
matemáticamente hablando podemos resolver el sistema de la siguiente forma:
a=6
Aplicando transformada inversa de laplace nos queda de la siguiente forma:
La respuesta ante una rampa unitaria es la siguiente:
Si A=1 ante un sistema rampa unitaria el comportamiento del sistema es el siguiente:
Si A=1
Entonces;
ENTRADA RAMPA UNITARIA
si se cambia la amplitud de la entrada
RESPUESTA TEMPORAL DE SISTEMAS DE SEGUNDO ORDEN.
Un sistema de segundo orden tiene como función de transferencia la siguiente ecuación:
Donde;
La ganancia en estado estacionario corresponde al valor constante que toma el sistema para un tiempo muy grande
Además de ello la respuesta del sistema depende de las raíces del denominador (polos del sistema) para una planta de segundo orden los polos se expresan como:
Los polos y la salida del sistema se representan de la siguiente forma
(td) tiempo de retardo= tiempo en que tarda la salida en alcanzar por primera vez que el 50% de yee
(TR) tiempo de crecimiento= es el tiempo transcurrido hasta que la salida cambia del 0 al 100% de yee es decir: yee=k
(tp) tiempo de pico= tiempo en el cual ymax alcanza su valor máximo
ts) tiempo de establecimiento= Tiempo transcurrido hasta que la salida alcanza un rango aproximado del 2% o 5% de yee
Para un criterio del 2%
visita nuestros contenidos relacionados con máquinas eléctricas.
visita nuestros contenidos relacionados con PLC
visita nuestros contenidos relacionados con mediciones e instrumentación.
CONTENIDOS MÁS RELEVANTES.