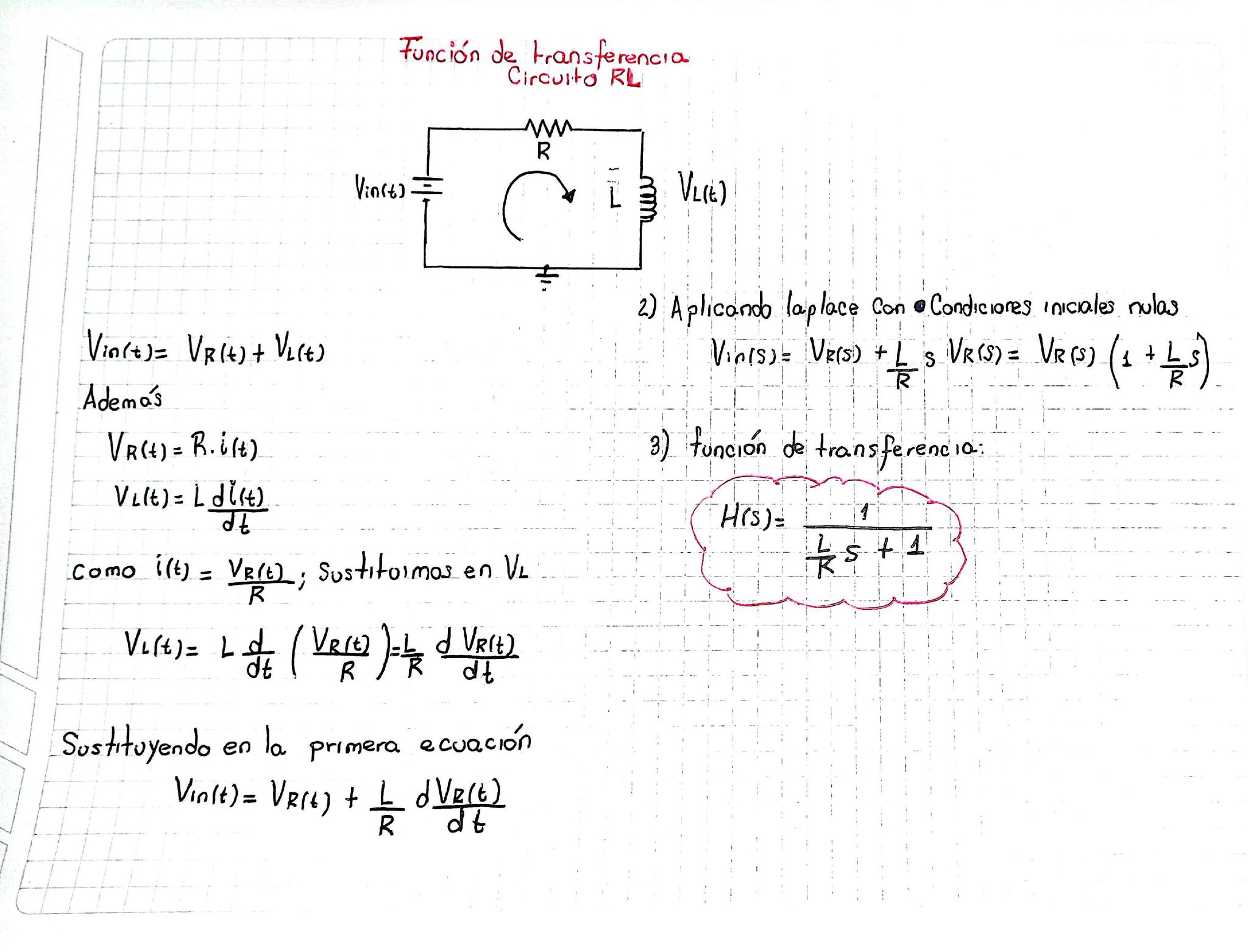
Este ejercicio resume de forma clara y ordenada cómo se obtiene la función de transferencia de un circuito RL en serie, partiendo desde las ecuaciones en el dominio del tiempo hasta llegar al dominio de Laplace.
La imagen muestra todo el proceso paso a paso, lo cual es ideal tanto para estudiantes como para ingenieros que quieren reforzar fundamentos de sistemas lineales.
Se comienza aplicando la ley de voltajes de Kirchhoff, donde el voltaje de entrada es la suma del voltaje en la resistencia y el voltaje en el inductor.
A partir de ahí, se expresan cada una de estas caídas de voltaje usando sus relaciones constitutivas básicas: el resistor se modela con la ley de Ohm y el inductor con su relación diferencial entre voltaje y corriente. Este punto es clave, porque conecta directamente el análisis de circuitos con ecuaciones diferenciales.
Luego, el ejercicio hace algo muy didáctico: elimina la corriente como variable intermedia y expresa todo en función del voltaje en la resistencia.
Esto permite obtener una ecuación diferencial de primer orden que relaciona la entrada con la salida. Aquí ya se empieza a ver claramente que el circuito RL es un sistema dinámico y no un simple circuito estático.
El siguiente paso es aplicar la transformada de Laplace bajo condiciones iniciales nulas, lo cual simplifica enormemente el análisis.
La ecuación diferencial se convierte en una ecuación algebraica en el dominio de la variable s, facilitando el despeje de la relación entre salida y entrada.
Finalmente, se obtiene la función de transferencia, que tiene la forma típica de un sistema de primer orden.
Esta expresión permite identificar directamente el comportamiento del circuito: su constante de tiempo, su respuesta transitoria y su respuesta en frecuencia. En términos de control y señales, este circuito se comporta como un filtro de primer orden.
En conclusión, la imagen no solo muestra el resultado final, sino que documenta todo el razonamiento físico y matemático detrás del modelo.
Es un excelente ejemplo de cómo pasar del circuito real a su representación en sistemas, algo fundamental en electrónica, control y procesamiento de señales.