Nota: Este laboratorio entrega los resultados del análisis de varias plantas o modelos por medio de MATLAB.

Objetivo: Identificación de tipo de modelo, obtención y análisis de la respuesta temporal de sistemas de primer orden y segundo orden ante diversos estímulos. Análisis de ubicación de polos y ceros (Usar comandos step y lsim).

1- Defina un modelo descrito en forma de función de transferencia para un sistema de segundo orden que presente estabilidad. Identifique:

a) que tipo de modelo es el anteriormente representado. (Estático o dinámico, justifique)

b) identifique y explique de que tipos de elementos se compone. (Dinámicos, estáticos)

2- Para un sistema de primer orden que presente estabilidad, estimule con una entrada escalón de magnitud 10 y obtener: a) La gráfica de la salida. b) El polo y su representación en el plano s.  c) Constante de tiempo y tiempo de establecimiento.

3- Si la entrada es una rampa de magnitud 7, obtener: a) La gráfica de la salida. b) El polo y su representación en el plano s.  c) Constante de tiempo y tiempo de establecimiento.

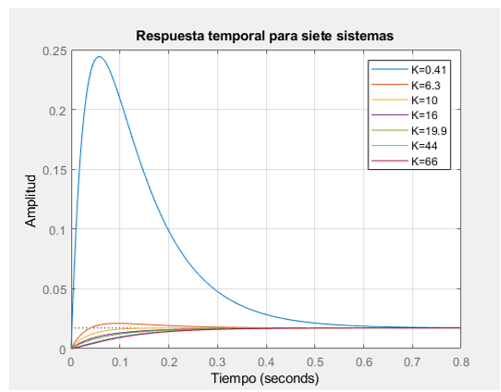
4-Grafique en una misma ventana de figura las salidas de los sistemas dados ante una entrada escalón unitario. Analice estas gráficas con respecto al tiempo de establecimiento y sobre impulsó máximo.

5- Para el siguiente modelo hallar:

 a) La gráfica de la salida. 

b) Los polos y su representación en el plano s. 

c) Tiempo de máximo pico, tiempo de establecimiento, y sobre impulso máximo.

Lo anterior para cada valor de d.

Análisis.

 

1. ¿Sistema es dinámico o estático?

El sistema eléctrico, es un sistema estático con condiciones iniciales iguales a cero. Cuando se le aplica un voltaje, el sistema se empieza a comportar como un sistema dinámico; debido a que tiene dos elementos del circuito que almacenan energía. 

Elementos dinámicos y estáticos:

—> Las dos resistencias son estáticas, porque no almacenan energía.

—>El condensador y la bobina son elementos dinámicos porque son elementos que tienen memoria.

—>El amplificador, es un elemento estático, porque es un elemento que no tiene memoria y no almacena energía, solo amplifica la señal de entrada.

INFORMACIÓN ENTREGADA POR MATLAB.

 

Nota: Como se puede ver en la imagen, el sistema es de segundo orden y estable porque sus polos se encuentran en el semiplano izquierdo.

2- Análisis matemático.

 

Gráfica de la respuesta en salida y la representación de los polos.

Sistema ante una entrada escalón de magnitud 10

El sistema es estable porque el polo está en el semiplano izquierdo (región de estabilidad).

Se estabiliza en la ganancia K=6,66 y con un ts (tiempo de establecimiento) de 2,66seg.

Nota: Las raíces geométricas es la representación gráfica de los polos.

 

Análisis matemático.

 

Gráfica de la respuesta en salida y la representación de los polos.

Análisis

                        Sistema ante una entrada rampa de magnitud 7

 

El sistema es estable porque uno de sus polos se encuentra en la región de estabilidad. 

Hay un polo que es igual a cero. Este polo se encuentra entre la región de estabilidad e inestabilidad. Esto quiere decir, que ante cualquier perturbación puede volver el sistema inestable. 

Nota: Las raíces geométricas es la representación gráfica de los polos.

 

4.

Análisis matemático.

 

Gráfica de la respuesta temporal ante un escalón unitario.

Análisis.

La k=0,41: Presenta un sobre impulso muy elevado. Su tiempo de establecimiento esta entre 0,6seg.

La k=0,63: Presenta un sobre impulso, pero no tan elevado. Su tiempo de establecimiento esta entre 0,3 o 0,4 seg.

Para las otras gráficas: No se puede apreciar un máximo sobre impulso. Su tiempo de establecimiento esta entre 0,3 o 0,4seg.

Hay que tener en cuenta que un máximo sobre impulso en la respuesta temporal puede ocasionar que la estabilidad de la magnitud se pierda, debido a que el sistema oscila de manera infinita.

5.

Sistema 1.

Análisis matemático.

Gráfica de la respuesta en salida y la representación de los polos.

Análisis

El primer sistema, es sub amortiguado. 

Es un sistema que tiene polos imaginarios; esto indica que el sistema va a presentar oscilaciones. 

Se estabiliza con un tiempo de establecimiento de 2.5seg.

 

Sistema 2.

 

Análisis matemático.

 

 

 

 

 

 

 

Gráfica de la respuesta en salida y la representación de los polos.

Análisis

El segundo sistema, es sobre amortiguado. Es un sistema que tiene polos en la región de estabilidad. Además, se estabiliza con un tiempo de establecimiento en 23 seg. Es posible evidenciar que la respuesta temporal de este sistema es más amortiguada. 

Código en Matlab

%Laboratorio 2
%Nat Arenas L

clc
clear all

K=menu(‘Seleccione menú’,’Primer punto’,’Segundo punto’,’Tercer punto’,’Cuarto punto’,’Quinto punto’,’SALIR’)

while(K)

if K==1

%Descripción del sistema eléctrico

figure(1)
imagen1=imread(‘Imagen_1.png’); %Lee la imagen del archivo
imshow(imagen1); %Muestra la imagen
imwrite(imagen1,’im1.png’);

figure(2)
imagen2=imread(‘Imagen_2.png’); %Lee la imagen del archivo
imshow(imagen2); %Muestra la imagen
imwrite(imagen2,’im2.png’);

figure(3)
imagen3=imread(‘Imagen_3.png’); %Lee la imagen del archivo
imshow(imagen3); %Muestra la imagen
imwrite(imagen3,’im3.png’);

end

if K==2
%———————————————————————————–
%Sistema de primer orden definido: Y(S)/R(S)=2/[2S+3]
%Normalizada:(2/3)/[(2/3)S+1]
%Con una entrada escalón de magnitud 10
%———————————————————————————–

disp(‘Sistema primer orden ante una entrada escalón magnitud 10’) %Poner texto

num=[2/3]; %Valor del numerador de la FT
den=[2/3 1]; %Valor del denominador de la FT
v1=ones(1,100); %Se crea un vector [100 veces 1]
t=[1:100]; %Se crea un vector[100 veces 1] para el tiempo
u=10*v1; %Se multiplica la magnitud con el vector creada
sis1=tf(num,den) %Permite crear la función de transferencia

%Respuesta temporal

subplot(2,2,1) %Pone la gráfica en la posición que se define
R1=lsim(sis1,u,t); %Grafica la respuesta temporal ante una entrada diferente
% al escalón unitario. U=10 es la entrada del
% sistema y t el tiempo
plot(t,u,’r–‘,t,R1,’b’) %Muestra la gráfica de la entrada y la salida
title(‘Respuesta ante un escalón con magnitud 10’) %Función para el título de la gráfica
xlabel(‘Tiempo’) %Función para el título del eje x
ylabel(‘Amplitud’) %Función para el título del eje y
grid on %Poner la cuadrícula

%Constante de tiempo y tiempo de establecimiento

disp(‘Constante de tiempo:’)
CT=den(1) %Extrae la primera posición del vector
disp(‘Unidad: Segundos’) %Extraer la primera posición del vector del denominador
disp(‘—————————————————–‘)
disp(‘Tiempo de establecimiento:’)
TE=4*CT %Halla el tiempo de establecimiento que son 5T
disp(‘Unidad: Segundos’)

%Graficar los polos del sistema

subplot(2,2,2) %Pone la gráfica en la posición que se define
polos=pole(sis1) %Muestra los polos del sistema
pzmap(sis1) %Gráfica los polos del sistema
title(‘Gráfica de los polos del sistema’) %Función para el título de la gráfica

%Graficar las raíces del sistema

subplot(2,2,3) %Pone la gráfica en la posición que se define
rlocus(sis1) %Gráfica las raíces del sistema
title(‘Lugar de las raíces geométricas’) %Función para el título de la gráfica
end

if K==3
%——————————————————-
%Sistema de primer orden definido: Y(S)/R(S)=2/[2S+3]
%Normalizada:(2/3)/[(2/3)S+1]
%Con una entrada rampa de magnitud 7
%——————————————————-

disp(‘Sistema primer orden ante una entrada rampa magnitud 7’) %Poner texto

num2=[2/3]; %Valor del numerador de la FT
den2=[2/3 1 0]; %Valor del denominador de la FT
sis2=tf(num2,den2)%Definir la función de transferencia
t2=0:0.1:3; %Se crea un vector de tiempo que va de 0 a 3 incrementando cada 0.1
u2=t2*7; %Se multiplica la magnitud 7 con el vector tiempo

%Respuesta temporal

subplot(2,2,1) %Pone la gráfica en la posición que se define
R2=lsim(sis2,u2,t2); %Grafica la respuesta temporal ante una entrada diferente a la rampa unitaria
plot(t2,u2,’r’,t2,R2,’b’) %Gráfica la entrada vs salida
title(‘Respuesta ante una rampa con magnitud 7’) %Función para el título de la gráfica
xlabel(‘Tiempo’) %Función para el título del eje x
ylabel(‘Amplitud’) %Función para el título del eje y
grid on %Poner la cuadrícula

%Constante de tiempo y tiempo de establecimiento

disp(‘Constante de tiempo:’)
CT2=den2(1) %Extrae la primera posición del vector
disp(‘Unidad: Segundos’) %Extraer la primera posición del vector del denominador
disp(‘—————————————————–‘)
disp(‘Tiempo de establecimiento:’)
TE2=4*CT2 %Halla el tiempo de establecimiento que son 5T
disp(‘Unidad: Segundos’)

%Graficar los polos del sistema

subplot(2,2,2) %Pone la gráfica en la posición que se define
polos=pole(sis2) %Muestra los polos del sistema
pzmap(sis2) %Gráfica los polos del sistema
title(‘Gráfica de los polos del sistema’) %Función para el título de la gráfica

%Graficar las raíces del sistema

subplot(2,2,3) %Pone la gráfica en la posición que se define
rlocus(sis2) %Gráfica las raíces del sistema
title(‘Lugar de las raíces geométricas’) %Función para el título de la gráfica

end

if K==4
%——————————————————————-
%Analizar los diferentes sistemas ante una entrada escalón unitario
%Y(S)/R(S)=[ 5/Z(S+Z) ]/(S+10)(S+29)
%——————————————————————-

disp(‘Analizar siete sistemas cuando se varia la Z’) %Poner texto

for i=1:7; %Se crea un ciclo for
z=[0.41 6.3 10 16 19.9 44 66]; %Se define un vector
num3=[5/z(i) 5]; %El valor del numerador de la FT
den3=[1 39 290]; %El valor del denominador de la FT
disp(‘Las funciones de transferencia de los sistemas son: ‘) %Poner un texto
sis(i)=tf(num3,den3) %Se genera la función de transferencia
hold on %Conservar la gráfica actual
step(sis(i)) %Gráfica de la respuesta temporal ante una entrada escalón
grid on %Poner cuadrícula
title(‘Respuesta temporal para siete sistemas’) %Poner el título a la gráfica
xlabel(‘Tiempo’) %Pone el título para el eje x
ylabel(‘Amplitud’) %Pone el título para el eje y
legend(‘K=0.41′,’K=6.3′,’K=10′,’K=16′,’K=19.9′,’K=44′,’K=66’) %Etiqueta de texto
end

end

if K==5
%—————————————————
%Hallar el modelo: Y(S)/R(S) =KWn^2/S^2+2dWnS+Wn^2
%Sistema sub-amortiguado de segundo orden
%—————————————————

disp(‘Sistema de segundo orden’)
modelo=menu(‘Dos sistemas’,’Sistema 1′,’Sistema 2′,’SALIR’)

while(modelo)

if modelo==1

%——————–
%Para d=0.64 R(S)=1/S
%——————–

%Los valores definidos
k=4.3;
Wn=2.5; %rad/seg
d=0.64;

num4=[k*Wn^2]; %El valor de numerador de la FT
den4=[1 2*d*Wn Wn^2]; %El valor del denominador de la FT
sis4=tf(num4,den4) %Genera la función de transferencia

%Respuesta temporal

subplot(2,2,1) %Pone la gráfica en la posición que se define
step(sis4) %Gráfica de la respuesta temporal ante una entrada escalón
title(‘Sistema subamortiguado ante una entrada escalón’) %Pone el título
xlabel(‘Tiempo’) %Pone el título para eje x
ylabel(‘Amplitud’) %Pone el título para eje y
grid on %Pone la cuadrícula

%Graficar los polos del sistema

subplot(2,2,2) %Pone la gráfica en la posición que se define
polos=pole(sis4) %Muestra los polos del sistema
pzmap(sis4) %Gráfica los polos del sistema
title(‘Gráfica de los polos del sistema’) %Función para el título de la gráfica

%Graficar las raíces del sistema

subplot(2,2,3) %Pone la gráfica en la posición que se define
rlocus(sis4) %Gráfica las raíces del sistema
title(‘Lugar de las raíces geométricas’) %Función para el título de la gráfica

%Tiempo de máximo pico, tiempo de establecimiento,sobreimpulso máximo

%Tp= Tiempo de máximo pico.
disp(‘——————————————‘) %Poner texto
disp(‘Tiempo máximo pico: ‘) %Poner texto
Tp4=(pi)/((Wn*(sqrt(1-d^2))))
disp(‘Unidad:Segundos’) %Poner texto

%Ts= Tiempo de establecimiento.
disp(‘——————————————‘) %Poner texto
disp(‘Tiempo de estblecimiento: ‘) %Poner texto
disp(‘——————————————‘) %Poner texto
disp(‘Criterio 2%: ‘) %Poner texto
Ts4_1=(4)/(d*Wn) %criterio 2%
disp(‘Criterio 5%: ‘) %Poner texto
Ts4_2=(3)/(d*Wn) %Criterio 5%
disp(‘Unidad:Segundos’) %Poner texto

%Mp= Máximo sobreimpulso
disp(‘——————————————‘) %Poner texto
disp(‘Máximo sobreimpulso: ‘) %Poner texto
Mp4=100*exp((-d*pi)/(sqrt(1-d^2)))
disp(‘Unidad: Porcentaje’)

end

if modelo==2

%——————–
%Para d=7.3 R(S)=1/S
%——————–

%Los valores definidos
k=4.3;
Wn=2.5; %rad/seg
d=7.3;

disp(‘——————————————‘) %Poner texto
disp(‘Sistema de segundo orden sobre-amortiguado’) %Poner texto
num5=[k*Wn^2]; %El valor de numerador de la FT
den5=[1 2*d*Wn Wn^2]; %El valor del denominador de la FT
sis5=tf(num5,den5) %Genera la función de transferencia

%Respuesta temporal

subplot(2,2,1) %Pone la gráfica en la posición que se define
step(sis5) %Gráfica de la respuesta temporal ante una entrada escalón
title(‘Sistema sobreamortiguado ante una entrada escalón’) %Pone el título
xlabel(‘Tiempo’) %Pone el título para eje x
ylabel(‘Amplitud’) %Pone el título para eje y
grid on %Pone la cuadrícula

%Graficar los polos del sistema

subplot(2,2,2) %Pone la gráfica en la posición que se define
polos=pole(sis5) %Muestra los polos del sistema
pzmap(sis5) %Gráfica los polos del sistema
title(‘Gráfica de los polos del sistema’) %Función para el título de la gráfica

%Graficar las raíces del sistema

subplot(2,2,3) %Pone la gráfica en la posición que se define
rlocus(sis5) %Gráfica las raíces del sistema
title(‘Lugar de las raíces geométricas’) %Función para el título de la gráfica

%Tiempo de máximo pico, tiempo de establecimiento,sobreimpulso máximo

%Tp= Tiempo de máximo pico.
disp(‘——————————————‘) %Poner texto
disp(‘Tiempo máximo pico: ‘) %Poner texto
disp(‘No hay tiempo pico’) %Poner texto

%Ts= Tiempo de establecimiento.
disp(‘——————————————‘) %Poner texto
disp(‘Tiempo de estblecimiento: ‘) %Poner texto
disp(‘——————————————‘) %Poner texto
Ts5=((4*2*d)/Wn)
disp(‘Unidad:Segudos’) %Poner texto

%Mp= Máximo sobreimpulso
disp(‘——————————————‘) %Poner texto
disp(‘Máximo sobreimpulso: ‘) %Poner texto
disp(‘No hay máximo sobre impulso’)

end

if modelo==3
break; %Salir del menú
end

modelo=menu(‘Dos sistemas’, ‘Sistema 1′,’Sistema 2′,’SALIR’)
end
end

if K==6
break; %Salir del menú
end

K=menu(‘Seleccione menú’,’Primer punto’,’Segundo punto’,’Tercer punto’,’Cuarto punto’,’Quinto punto’,’SALIR’)
end

CONTENIDOS MÁS RELEVANTES.