visita nuestros contenidos relacionados con PLC
visita nuestros contenidos relacionados con mediciones e instrumentación.
Actualmente en la industria los controladores más implementados en los equipos y sistemas son los discretos o digitales.
Todo proceso va ligado a un modelo matemático que busca describir la dinámica del sistema, llámese: temperatura, presión, nivel, caudal, mecánico, velocidad por mencionar las variables más críticas.
En la industria es posible hasta los tiempos de hoy presenciar procesos totalmente analógicos, algo que no está mal.
Sin embargo, gracias al maravilloso mundo de los microcontroladores y la aparición de nuevos entornos de desarrollo libres, de fácil acceso como son: Arduino, Raspberry pi, Beaglebone y otras interfaces; es posible implementar leyes y algoritmos que controlen un proceso en particular.
Los controladores modernos también poseen estas soluciones particulares para la industria como lo es el auto-sintonizado o auto-tuning.
Tal vez este no sea un tema de importancia para los empíricos o técnicos que se mueven en el mundo de la instrumentación, el control y la electrónica pero es importante saber de donde salen las cosas y el porqué de ellas.
Quiero decirles en este post que cualquiera que esté interesado en aprender, investigar y apropiarse de este conocimiento es bienvenido en la página y con el mayor de los gustos le entrego este material que hace parte de mi formación como ingeniero en instrumentación y control.
FUNCIÓN DE TRANSFERENCIA DE PULSO.
La forma tradicional para hacer modelamiento de sistemas lineales es utilizar y apropiarse del concepto de función de transferencia con el fin de que usted pueda representar las relaciones entrada-salida de las variables de proceso.
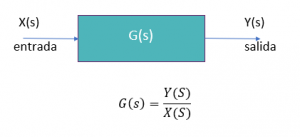
Para un sistema en tiempo continuo, lineal e invariante en el tiempo, la función de transferencia se define como la relación de la transformada de laplace de salida y la transformada de laplace de la entrada asumiendo que las condiciones iniciales sean iguales a cero.
Esa función de transferencia que hemos venido mencionando se expresa solo como función de la variable compleja S.
Por conocimiento, ya sabemos que la representación de un sistema continuo es tal cual como se muestra en la figura 1.
¿QUE SE NECESITA PARA QUE SEA UNA FUNCIÓN DE TRANSFERENCIA DE PULSO?
Idealmente un muestreador incluyendo una función de transferencia la cual es modelada por un fenómeno.
Una Función de transferencia de pulso también es acompañada por un retenedor preferiblemente de orden cero que son con los cuales se trabajarán en estos contenidos y en este post en particular.
Entender los conceptos matemáticos de la transformada Z (fundamental)
tablas de transformada Z y Zm (Z-modificada).
Esto será un poco difícil.

básicamente consiste en encontrar la función de transferencia de la función de la figura anterior en términos de Z
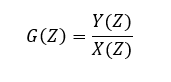
FUNCIÓN DE TRANSFERENCIA DE PULSO CON RETENEDOR.
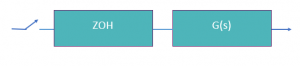
La función matemática del retenedor (ZOH) es la siguiente:
La ecuación representada en color ROJO, representa la transformada Z que modela a un RETENEDOR.
EJERCICIOS DE FUNCIÓN DE TRANSFERENCIA DE PULSO.
1. Calcular la función de transferencia de pulso (FTP) del siguiente sistema:

PASOS.
1- La planta representada en el bloque no posee retardo, por lo tanto es NECESARIO calcular esta variable. (se cierra el lazo).
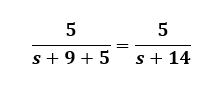
2- Una vez cerrado el lazo, el modelo se debe NORMALIZAR
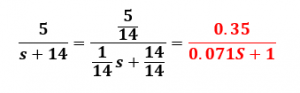
3- Una vez normalizada la ecuación, se procede a calcular y a seleccionar el periodo de muestreo por el criterio de T equivalente.
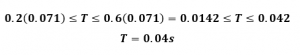
Para este ejercicio en particular, en el rango obtenido se seleccionó un periodo de muestreo de 0.04 segundos.
4- posteriormente y en LAZO ABIERTO (OJO), se procede a aplicar transformada Z a la función de transferencia. El valor de T será reemplazado mediante las transformadas z.
EN ESTE ENLACE PUEDES DESCARGAR LAS TABLAS DE LA TRANSFORMADA Z Y Z MODIFICADA
5- resolviendo el ejercicio tenemos:
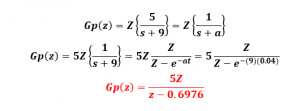
Gráficamente en MATLAB, se ve de la siguiente forma.

El algoritmo empleado para graficar es el siguiente.
clc
clear all
f = tf( 5, [1 9])
hd = c2d(f,0.04)
step(f,»,hd,’-‘)
grid on
EJERCICIO 2.
Encontrar la función de transferencia de pulso del sistema.
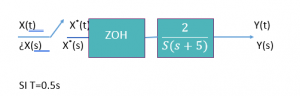
PASOS.
1- Para este ejercicio, no es necesario calcular el periodo de muestreo puesto que ya lo han asignado por defecto. Lo primero que se debe hacer es discretizar el modelo.
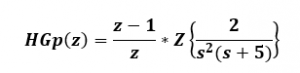
2- en las tablas de la transformada z, buscamos la forma que más se asemeja a la función de transferencia en tiempo continuo.
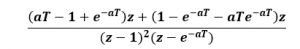
3- Realizamos las operaciones necesarias para resolver el ejercicio.
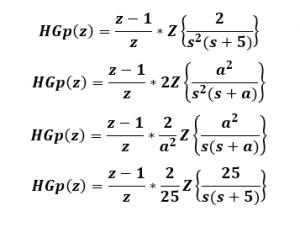
4- lo que se debe hacer posteriormente es realizar las operaciones necesarias y reemplazar en la transformada Z
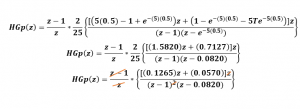
5- finalmente se procede a resolver la ecuación en el denominador y esta queda de la siguiente forma:
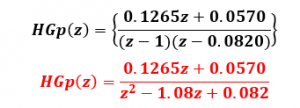
El algoritmo en MATLAB es el siguiente:
clc
clear all
f = tf( 2, [1 5 0])
hd = c2d(f,0.5)
step(f,’-‘,hd,’-‘)
grid on
se comprueba la función de transferencia obtenida matemáticamente vs la obtenida en MATLAB.

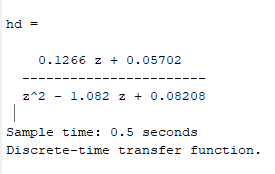
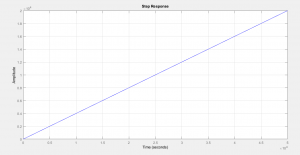
El gráfico obtenido en MATLAB es el siguiente:
EJERCICIO 3.
Encontrar la función de transferencia de pulso para el sistema representado en la siguiente figura:
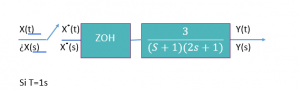
PASOS.
1- Para este ejercicio, no es necesario calcular el periodo de muestreo puesto que ya lo han asignado por defecto. Lo primero que se debe hacer es discretizar el modelo.
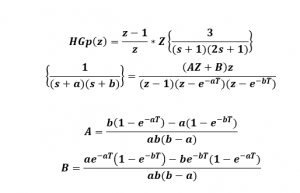
2- realizamos las operaciones necesarias para resolver el ejercicio.
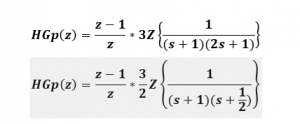
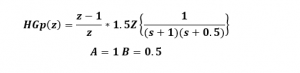
3- encontramos los valores de A y B
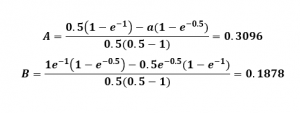

El algoritmo en MATLAB es el siguiente
clc
clear all
f = tf( 3, [2 3 1])
hd = c2d(f,1)
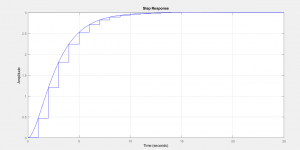
step(f,’-‘,hd,’-‘)
grid on
Los resultados por consola son los siguientes:
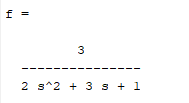
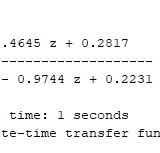
La respuesta del modelo es el siguiente:
visita nuestros contenidos relacionados con máquinas eléctricas.
CONTENIDOS MÁS RELEVANTES.