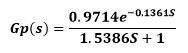Saludos compañeros. Hoy vamos a efectuar adquisición y filtrado de datos en un modelo matemático que describe el comportamiento de una planta de presión. Primeramente, se va a calcular el periodo de muestreo con el cual se realizó la toma de datos utilizando el criterio de ancho de banda.
El modelo de la planta es el que se describe a continuación.
Esta ecuación obtenida corresponde a un modelamiento matemático previo de una planta de presión en lazo abierto.
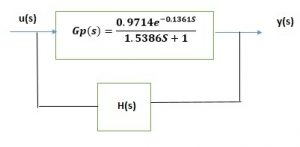
Para resolver el ejercicio, debemos prescindir del retardo, esto quiere decir que el valor de theta es igual a cero, es decir que la planta no posee retardo, además de ello se debe aplicar re-alimentación al modelo matemático.
Procederemos a cerrar el lazo.
Cuando se realimenta el lazo, por álgebra de bloques nos queda la siguiente ecuación.
Convirtiendo al dominio frecuencial, R(s)=Rw(s)
Habíamos asumido una planta sin retardo, por lo tanto, el modelo de la planta de presión quedará de la siguiente forma:
| ECUACION 1 |
Aplicando la ecuación de realimentación del lazo:
en base al periodo de muestreo, se procede a calcular el circuito de filtrado de datos.
FILTRADO DE DATOS: hay un esquema electrónico estándar para hacer filtros de la información a procesar entregada por la planta no obstante el filtrado de dicha información es posible implementarlo por software (Matlab, labview)
Procedemos con el cálculo de la reactancia capacitiva que nos ayudará a determinar el valor de la resistencia.
A continuación, presentamos la tabla de sintonización Ziegler-Nichols para plantas de primer orden con retardo, esto con el fin de ajustar los parámetros P-PI-PID para la planta de presión y seleccionar el mejor controlador.
CONTENIDOS MÁS RELEVANTES.