En este sencillo post, haremos un ejercicio simple de análisis con dos resistencias en paralelo.
Circuitos en paralelo: Ejercicio con dos resistencias.
Para este ejercicio se solicita hallar: RT e IS
Adicional a eso, se debe encontrar la corriente I1 e I2
Se debe demostrar que Is = I1 +I2
Se debe calcular la potencia disipada en toda la carga resistiva
Se debe calcular la potencia disipada por cada una de las resistencias
Finalmente se debe calcular la potencia entregada por la fuente.
SOLUCIÓN AL PROBLEMA.
Inicialmente tenemos el ejercicio propuesto.
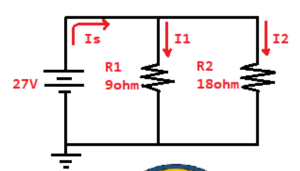
Se procede a calcular inicialmente la resistencia equivalente RT
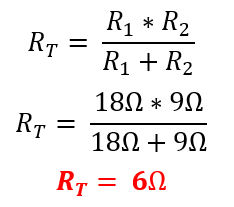
Una vez calculado el valor de RT, se procede con el cálculo de la corriente total IS
Teniendo en cuenta que el voltaje en paralelo es el mismo para todos los elementos que conforman el circuito, se procede a decir lo siguiente:
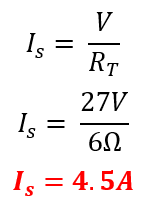
Una vez calculado el valor de Is se procede con el cálculo de I1 e I2 con el fin de comprobar la ley de corriente de Kirchhoff.
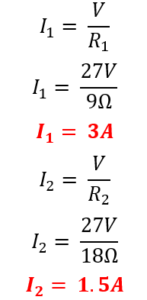
Una vez calculados los valores de la corriente I1 e I2, Se procede a expresar la siguiente ecuación de ley de corriente de Kirchhoff.
![]()
Si reemplazamos los valores obtenidos de IS, I1 e I2 se puede apreciar que la corriente es igual y por lo tanto se cumple la ecuación planteada anteriormente.
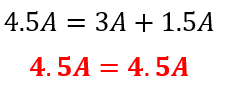
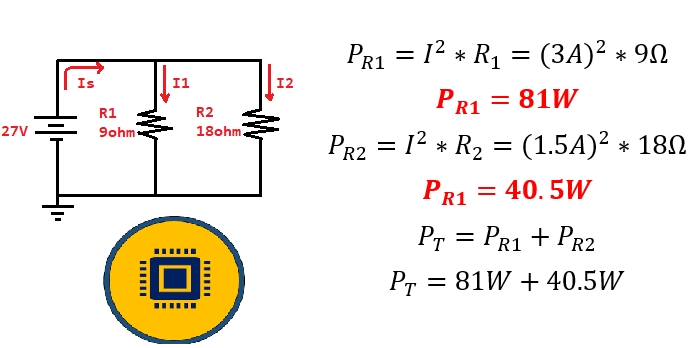
Teniendo los valores de corriente anteriormente mencionados, es posible calcular la potencia en la carga resistiva equivalente, así como la potencia en cada una de las resistencias del circuito.
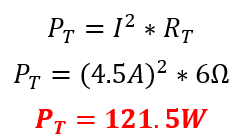
Para comprobar el cálculo de los valores de potencia total PT, se procede a calcular los valores de potencia disipada en cada una de las resistencias del circuito. El valor que se debe obtener a la salida es equivalente a PT =121.5W
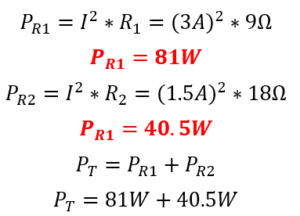
![]()
Como se puede apreciar, la potencia total disipada es 121.5W con la suma de las potencias para cada una de las resistencias vs la resistencia equivalente.
Finalmente se calculó la potencia entregada por la batería de 27V

Y con esto se le da fin al ejercicio del análisis del circuito de dos resistencias en paralelo.
En otros posts se estarán realizando más ejercicios de análisis de circuitos en paralelo.
CONCLUSIONES FINALES.
Recuerde que, para realizar análisis de circuitos en paralelo, tenga en cuenta que el voltaje es el mismo para todos los elementos que conforman el circuito.
La variable: Corriente eléctrica, no es igual para todos los elementos del circuito y dependerá básicamente de la resistencia interna que posea el dispositivo a conectar.
Las redes eléctricas que usted encuentra en las casas y en las grandes industrias, se encuentran conectadas en paralelo. Es muy raro encontrar un circuito serie en una instalación residencial, comercial e industrial.
En diseño electrónico, los componentes electrónicos de igual forma se encuentran distribuidos en paralelo.
Todos estos análisis deben ser aterrizados empleando la simulación electrónica y las prácticas de laboratorio.
DESCARGA EL ARCHIVO EN PDF AQUI
CONTENIDOS RELEVANTES.